Episodi 3. Regle i Compàs

Parlarem de tres problemes de la Grècia clàssica sobre construccions amb regle no marcat i compàs: la quadratura del cercle, la trisecció de l’angle i la duplicació del cub. Caracteritzarem els nombres constructibles, i veurem que aquests problemes no tenen solució. Veurem també que si el regle és marcat aleshores podem trisecar l’angle i també duplicar el cub.

3.1 El problema

Els grecs es van interessar molt per les construccions amb dos instruments molt simples: per una banda, el que habitualment s’anomena regle, i que vol dir simplement un regle sense cap mena de marca. Ens permet, donats dos punts del pla, traçar la recta que els uneix. El segon instrument és el compàs. Donats dos punts podem fixar l’obertura, i donat un tercer punt (que pot coincidir o no amb els anteriors) podem traçar un arc de circumferència amb el radi fixat prèviament, i el centre aquest tercer punt.

Hi ha tres problemes clàssics que ens proposem estudiar:

1. “Duplicació del cub”: donat un cub, podem construir-ne un altre de volum exactament el doble?
2. “Trisecció de l’angle”: donat un angle \(\theta\), podem construir l’angle \(\theta/3\)?
3. “Quadratura del cercle”: donat un cercle, podem construir un quadrat d’àrea igual a la del cercle donat?

Donada una longitud inicial (que definirem com a \(1\)), direm que un nombre real \(\alpha\) és constructible si podem construir un segment de longitud \(\alpha\) mitjançant una successió finita d’operacions amb regle i compàs. Tenim els quatre tipus d’operacions següents:

1. Unir dos punts per una recta.
2. Trobar el punt d’intersecció de dues rectes.
3. Dibuixar un cercle amb centre i radi donats.
4. Trobar els punts d’intersecció d’una recta amb un cercle, o de dos cercles.

Podeu jugar a fer construccions amb regle i compàs amb el joc online Euclidea.

3.2 La (no) solució

Comencem veient que els nombres constructibles són un cos.

Proposició 3.1 Els nombres constructibles formen un subcos de \(\RR\).

Prova. Cal donar construccions de la suma, resta, producte i divisió de nombres ja construïts. Mentre que la suma i la resta són òbvies, la multiplicació i divisió es poden obtenir aplicant proporcionalitat, com veiem en els diagrames d’aquí sota.

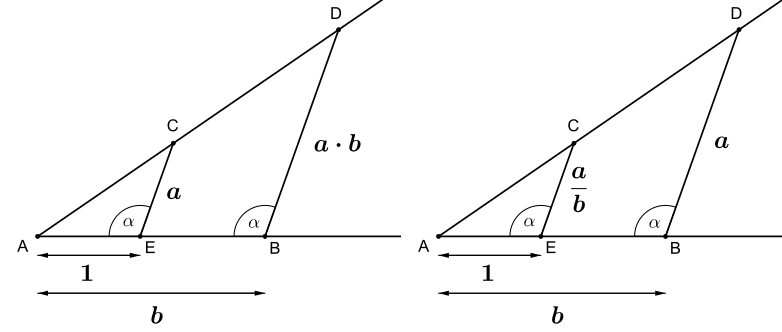
Figura 3.1: Multiplicació i divisió amb regle i compàs.

És fàcil veure que també podem prendre arrels quadrades, com s’indica al següent exercici.

Exercici 3.1 Demostreu que si el diàmetre de la circumferència és \(\alpha+1\), aleshores el segment vertical indicat mesura \(\sqrt{\alpha}\).

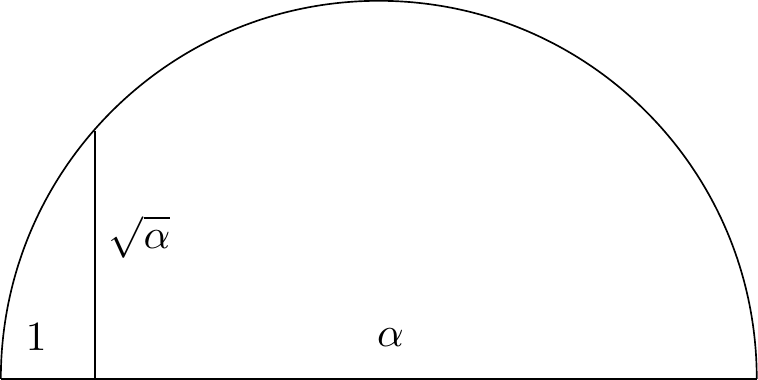
Figura 3.2: Construcció de l’arrel quadrada amb regle i compàs

Fent servir l’equació d’un cercle de radi \((x_0,y_0)\) i radi \(r\) \[ (x-x_0)^2 + (y-y_0)^2 = r^2, \] podem veure que les coordenades de la intersecció amb una recta (posem amb equació \(ax+by=c\)) pertanyen a una extensió quadràtica del cos \(\QQ(x_0,y_0,r,a,b,c)\). També podem comprovar-ho pel cas de la intersecció de dos cercles. Resumint, si \(\alpha\) és constructible en \(n\) passos a partir de punts en un cos \(F\), aleshores hi ha una successió de cossos \[ F=F_0\subseteq F_1\subseteq F_2\subseteq F_n, \] amb \([F_{i+1}\colon F_i] \leq 2\), tals que \(\alpha\in F_n\). En particular, \(\alpha\) és un nombre algebraic sobre \(F\) de grau una potència de \(2\).

D’aquí en deduïm directament el següent teorema (on haurem d’assumir que \(\pi\) és transcendent, cosa que no demostrem).

Teorema 3.1 Cap dels tres problemes clàssics no és resoluble.

Prova. Per la duplicació d’un cub de costat \(1\) ens caldria construir \(\sqrt[3]{2}\), que té grau \(3\) i, per tant, no és constructible.

Si un angle \(\theta\) és constructible, aleshores fàcilment veiem que \(\cos(\theta)\) i \(\sin(\theta)\) també són constructibles, simplement traçant la perpendicular a un dels dos raigs de l’angle. Veurem doncs que \(\alpha=2\cos(\pi/9)\) no és constructible. Recordem la fórmula del cosinus de l’angle triple, que s’obté aplicant dues vegades la de l’angle doble: \[ \cos(3\theta) = 4\cos^3(\theta)-3\cos(\theta). \] Com que \(\cos(\pi/3)=1/2\), substituint \(\theta=\pi/9\) a la fórmula anterior obtenim la relació \[ \alpha^3 - 3\alpha -1 =0. \] El polinomi \(x^3-3x-1\) és irreductible (substituint \(x-2\) obtenim un polinomi \(3\)-Eisenstein) i per tant \(\alpha\) té grau \(3\) i no és constructible.

Finalment, per la quadratura del cercle de radi \(1\) hauríem de construir un quadrat de costat \(\sqrt{\pi}\). Però aleshores també podríem construir \(\pi\), que és transcendent (com hem dit, no ho demostrem).

Més endavant estudiarem quins angles són constructibles, en general. Per ara, podem demostrar el següent:

Teorema 3.2 Sigui \(t\) un enter. L’angle de \(t\) graus és constructible si i només si \(t\) és un múltiple de \(3\).

Prova. Hi ha construccions molt antigues del pentàgon regular (\(72^\circ\)), ja que \[ \cos(72^\circ) = \frac{1}{4} \, \sqrt{5} - \frac{1}{4}. \]

Aquí en tenim un exemple.

Exercici 3.2 En aquest dibuix, comencem amb els punts \(A\) i \(B\). Podem dibuixar els cercles \(1\) i \(2\), dibuixar el cercle \(3\), obtenint els punts \(C\) i \(D\). La mediatriu del segment \(AB\) talla el cercle \(3\) en el punt \(F\), i podem construir les rectes \(CF\) i \(DF\), que donen lloc als punts \(M\) i \(N\).

Si volem construir el cinquè vèrtex del pentàgon, només hem de traçar els cercles \(4\) i \(5\).

Demostreu que aquesta construcció resulta en un pentàgon regular.

Figura 3.3: Construcció d’un pentàgon regular amb regle i compàs.

Encara és més fàcil construir el triangle equilàter (\(30^\circ\)), ja que \(\cos(30^\circ)=\sqrt{2}/2\). Com que podem bisectar qualsevol angle, també podem construir \(18^\circ\) i \(15^\circ\). Finalment, com que \(3=18-15\) també podem construir l’angle de \(3^\circ\). És clar que no podem construir ni \(2^\circ\) ni \(1^\circ\), perquè aleshores podríem construir també qualsevol múltiple d’aquests i, per tant, podríem construir \(20^\circ\), que ja sabem que no és possible.

3.3 Construccions amb regle marcat i compàs

És important adonar-se que amb molt poc més aleshores algunes construccions clàssiques esdevenen molt senzilles. Aquí veurem que si el regle té dues marques a una distància qualsevol, aleshores podem trisecar l’angle i duplicar el cub.

Exercici 3.3 (Trisecció d'un angle) En el dibuix d’aquí sota, s’ha començat amb un angle \(a\) amb centre \(B\). Suposem que el regle té dues marques a una certa distància, que serà la nostra unitat. Fem un cercle de radi aquesta unitat, i tracem una recta pel punt A de manera que les dues marques del regle estiguin una sobre el cercle (punt \(C\)) i l’altra sobre la recta donada (punt \(D\)).

Demostreu que l’angle \(b\) és igual a \(\frac{a}{3}\) (aquesta construcció ja l’havia trobat Arquímedes!).

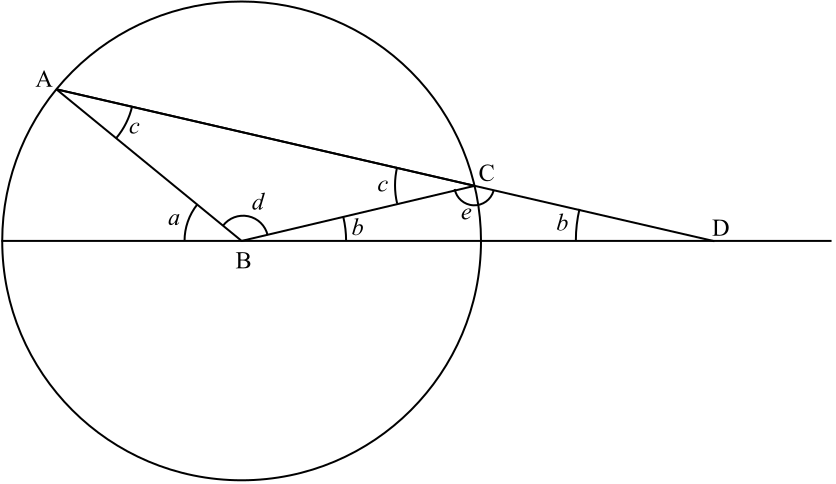
Figura 3.4: Trissecció d’un angle amb regle marcat i compàs.

Exercici 3.4 (Duplicació del cub) Comencem amb un triangle equilàter \(ABC\), de costat una unitat fixada per les marques del regle, que anomenarem \(1\). Perllonguem el costat \(AB\) en una unitat per construir \(D\). Considerem els rajos \(\vec{DC}\) i \(\vec{BC}\). Ara fem servir el regle marcat per construir una recta pel punt \(A\) de manera que la intersecció amb els dos rajos anteriors doni lloc a un segment \(GH\) de longitud \(1\). Demostreu que el segment \(AG\) mesura \(\sqrt[3]{2}\).

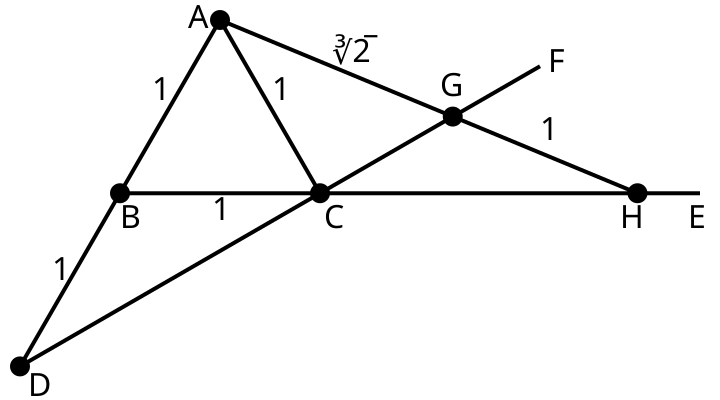
Figura 3.5: Duplicació del cub amb regle marcat i compàs.